The 3D printing process begins with a 3D model of the object, usually created by computer-aided design (CAD) software. One of the widely used open-source CAD programs is OpenSCAD.

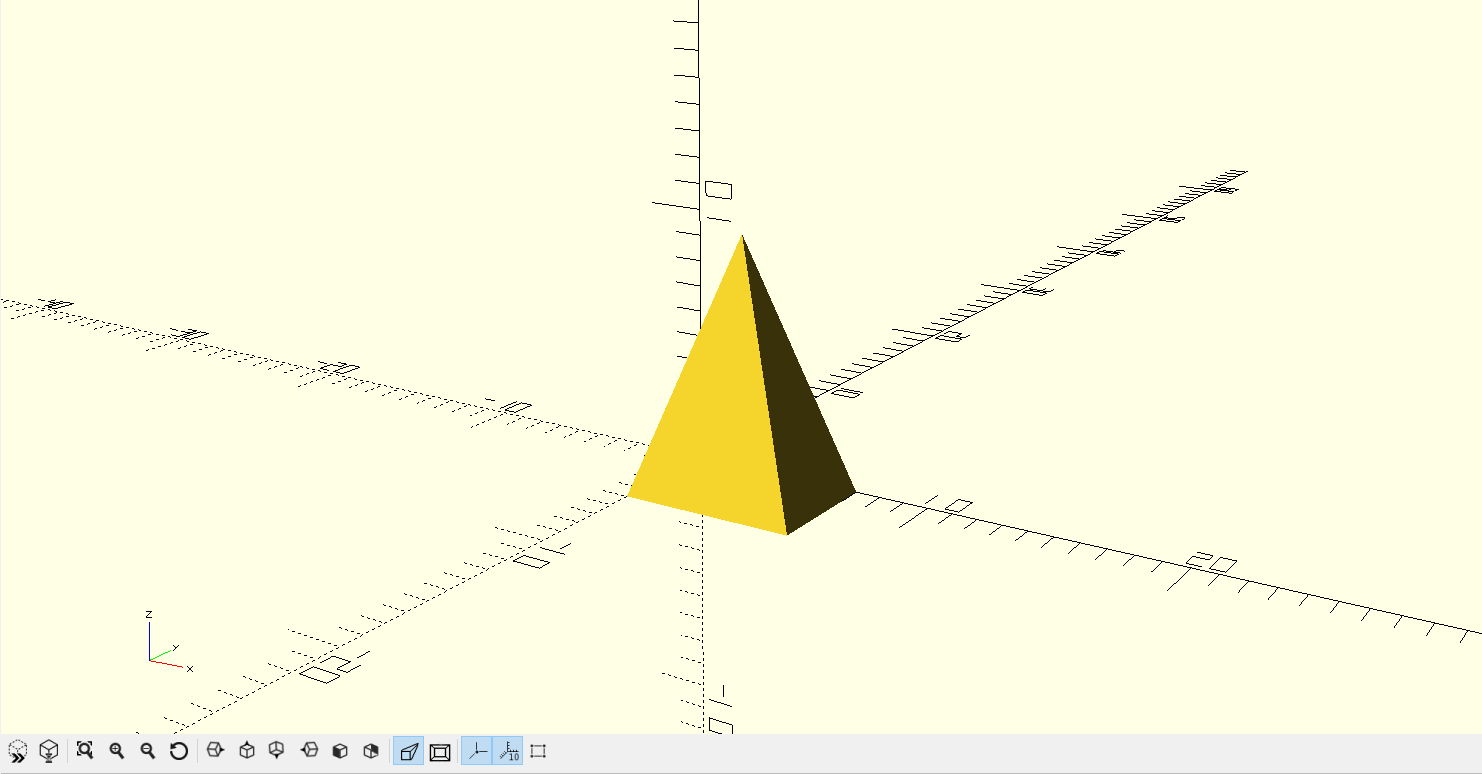
Here is an example of a simple 5 x 7 x 10 pyramid created using OpenSCAD.

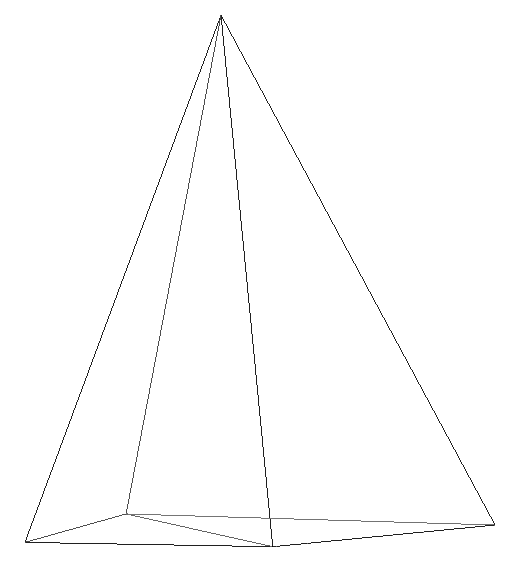
An STL (“StereoLithography”) file is a triangular representation of a 3-dimensional surface geometry. Developed in 1987 for 3D Systems, the STL format was designed as a standard format to allow data movement between CAD programs and stereolithography machines. The surface is tessellated or broken down logically into a series of small triangles (facets). Any shape can be used for tessellations, but STL format uses triangles. This triangular mesh is most often derived from the surface – and only the surface – of a 3D CAD designed object.

For a simple 3D object such as our pyramid, the entire surface can be covered with just 6 triangles; 4 for each side of the pyramid and 2 to cover the bottom rectangular base.

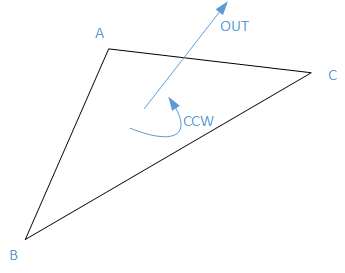
In an STL file, each and every triangle ‘facet’ is defined in terms of the coordinates of its three vertices. In addition a normal vector (a line perpendicular to the triangle and with a length of 1.0) is included so that the inside and outside of each facet are clear. Further, the vertices are listed in counterclockwise order when looking at the object from the outside (right-hand rule).

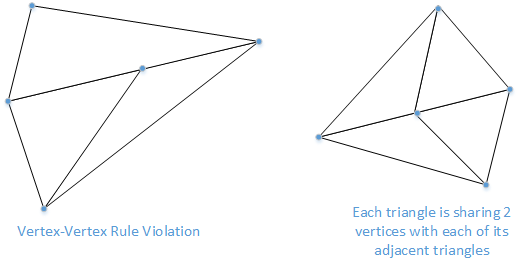
Also, Each triangle must share two vertices with each of its adjacent triangles (vertex-vertex rule). In other words, a vertex of one triangle cannot lie on the side of another. This ensures that there are no gaps/uncovered surfaces.

The STL file Format

An STL file could be both in ASCII and binary format, but binary files are more common since they are more compact. To understand STL better, lets look at the ASCII stl file for our simple pyramid:

solid SimplePyramid
 facet normal 0 0 -1
  outer loop
  vertex 0 0 0
  vertex 7 -5 0
  vertex 0 -5 0
  endloop
 endfacet
 facet normal 0 0 -1
  outer loop
  vertex 0 0 0
  vertex 7 0 0
  vertex 7 -5 0
  endloop
 endfacet
 facet normal -0.943858 0 0.33035
  outer loop
  vertex 0 0 0
  vertex 0 -5 0
  vertex 3.5 -2.5 10
  endloop
 endfacet
 facet normal 0 0.970143 0.242536
  outer loop
  vertex 0 0 0
  vertex 3.5 -2.5 10
  vertex 7 0 0
  endloop
 endfacet
 facet normal 0 -0.970143 0.242536
  outer loop
  vertex 0 -5 0
  vertex 7 -5 0
  vertex 3.5 -2.5 10
  endloop
 endfacet
 facet normal 0.943858 0 0.33035
  outer loop
  vertex 7 0 0
  vertex 3.5 -2.5 10
  vertex 7 -5 0
  endloop
 endfacet
endsolid SimplePyramid

Here, each of the six triangles is represented by a facet. The file simply contains the normal vector and the 3 vertex coordinates for each triangle.

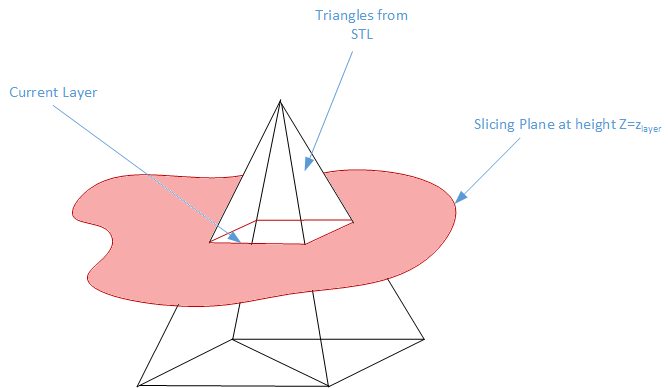
Slicing the STL model

Modeling your shape is only the first step of 3D printing. You need to process the resulting STL with a slicer program that will cut your solid into thin slice and decide how to print them. To visualize the layers, here is our pyramid STL file sliced using Slic3r:

Lets look at how exactly this slicing happens:

Each slicing plane can be considered as an infinite plane at a specific height Z. The slicing problem now boils down to finding the intersection of all the triangles in STL with that plane at height Z. We could use a brute force method and check if each triangle is intersecting the current plan. This is easy for our pyramid as it only has 6 triangles. This is obviously not optimal for more complicated objects with thousands of triangles. We have to weed out most of the candidates otherwise we’ll spend ages processing the file.

Determining triangles at each layer

There are many solutions to the optimization problem. Here is a simple algorithm that was (probably) used during the early days of slic3r:

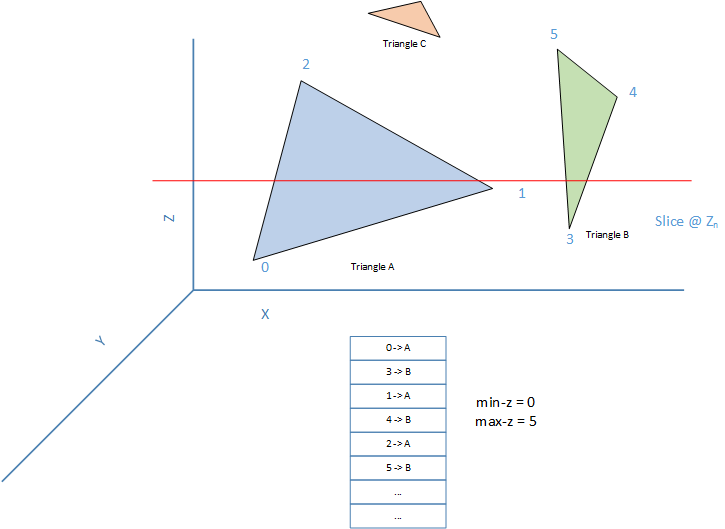
1. Make a list of all the vertices and the triangles they belong to.
2. Sort the list by the z value of the vertices. a. The beginning of the list has the smallest Z value (min-z) and the end has the largest z (max-z). b. The object to be printed needs to be sliced from min-z to max-z.
3. A triangle is considered to be active if it intersects with the current layer z-plane. For example, in the picture below, Triangles A & B are active while C is not.
4. For each triangle we also keep track of how many of the triangles vertices the slicing layer has crossed. The triangle is active when count is 1 or 2 and inactive when count is zero or 3.

Here is the pseudocode for slicing:

[sorted list] // list of vertices and their triangle, sorted by their z values.
[active triangles] <- {} // All the triangles that the current z-plane intercepts. 
[vertex seen count] <- {} // For each triangle, how many of its vertices have we already seen? 
next_layer_z = min-z + layer_height // Start from min-z + layer_height
for(V = next vertex in [sorted list]) { 
    Z <- z value of vertex V 
    T <- Triangle this vertex V belongs to

    // The current layer is still lower than this new vertex.
    // Create all layers until we reach this vertex. 
    // Since the triangles remains the same between two adjacent Z heights, 
    // we can keep adding the same active triangles to the layers.
    while(Z > next_layer_z) {
          // Add all triangles in the active set of triangles we are slicing to the current layer
          current_layer <- all triangles in [active triangles]

          // Save the current layer 
          all_layers <- current_layer

          // advance to next layer height
          next_layer_z+=layer_height;
       }

       // The slicing plane has now reached the new vertex V. 
       // Add its triangle to the list of active triangles
       // NOTE: this triangle could already be active.
       [active triangles] <- T

       [vertex seen count for T] += 1

       // If this is the last vertex of this triangle, we have crossed this triangle
       // Remove it from the list of active triangles.
       if [vertex seen count for T] == 3
           remove T from [active triangles]                   
}

Triangle intersection with a plane

Now that we have the list of triangles at each layer, we have to determine the intersection point and the line segment created by the intersection.

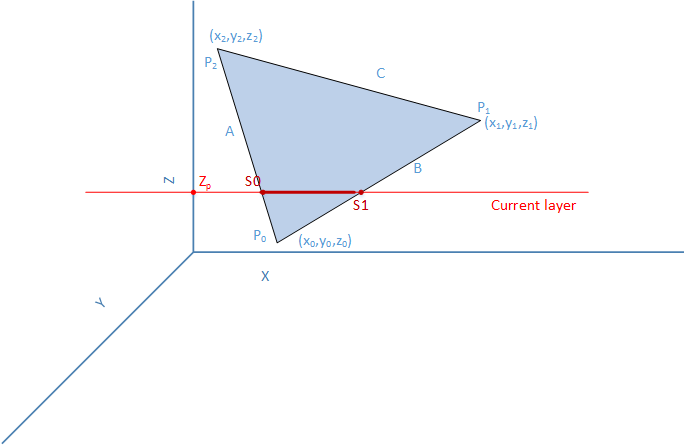
To calculate the intersection points, we first need to know which edges of the triangle intersect the slicing plane. Consider the triangle show below.

If the vertices of the triangle are sorted by their z height, the intersection points can be easily calculated.

1. As long as Z0 <= Z1 <= Z2
2. If Z1 > Zp, then edges A & B intercept the slicing plane
3. If z1 <= Zp, then edges A & C intercept the slicing plane.

With the edges determines, calculating the segment vertices S0 & S1 is a trivial projection of a triangle on a plane. For example, with edge A, any point on the line can be represented as a linear interpolation between P0-P2. Hence,

S0 = P0 + t * (P2 - P0) Where t is the projective length 
t=(Zp-Z0)/(Z2-Z0)

S0x = X0 + t * (X2 - X0) 
S0y = Y0 + t * (Y2 - Y0) 
S0z = Zp

Determining the interception polygon

For an object to be printed, the printer needs to make a continues movement to get the best and fast prints. What we have so far is a list of segments at each layer. Printing these segments as is will make the printer head skip/travel from segment to segment in a random order. We need to convert this random set of segments into a closed/open polygon by connecting them together. We can do this by sorting/connecting the segments so that neighboring segments are printed in order. Here is a simple algorithm for this:

1. For each segment, determine its left and right segment based on the vertices it shares with them.
2. Assign an index to each segment: a. segmentIndex = 0 if first segment b. Segmentindex = left segmentindex + 1
3. Sort all the segments based on this index. By implicitly sharing a common vertex with its neighbor, the segments form a continuous movement of the print head.

Generating Gcodes

Generating Gcodes is now just a matter of transforming each segment into a printer head movement with the right amount of extrusion of filament. Here is an example for layer 0: (Look at the comments for more explanation.)

Layer 0 segments:
Segment 0: (0.455000, -4.575000, 0.300000) -> (0.455000, -0.425000, 0.300000)
Segment 1: (6.545000, -0.425000, 0.300000) -> (0.455000, -0.425000, 0.300000)
Segment 2: (6.545000, -4.575000, 0.300000) -> (0.455000, -4.575000, 0.300000)
Segment 3: (6.545000, -4.575000, 0.300000) -> (6.545000, -0.425000, 0.300000)

Printing Layer 0:
; Reset the Extruder before printing the layer
G92 E0

; position the print head at the right height (0.3mm) for layer 0.
; Set the extrusion rate to 500mm/minute
G1 Z0.300000 F500.000000

; Move the print head to start of first segment. 
; We pick the vertex that is closest to the print head to reduce the amount
; of travel. In this case (0.455000, -0.425000) is the closest to (0, 0), so we move there.
; Segment 0: (0.455000, -0.425000, 0.300000) -> (0.455000, -4.575000, 0.300000)
G1 X0.455000 Y-0.425000

; Move the print head to end of the segment, while extruding at 1.079165mm of filament.
G1 X0.455000 Y-4.575000 E1.079165

; In the previous segment, we stopped at (0.455000, -4.575000). We find the closest 
; vertex of neighboring segment  (6.545000, -0.425000, 0.300000) -> (0.455000, -0.425000, 0.300000)
; and move there without extruding. 

; Retract filament before we move (so there is no extrusion)
G1 F1800.0 E0.079165

; Move to next closest vertex.
G1 X0.455000 Y-0.425000

; Resume extrusion at the same rate as before
G1 F1800.0 E1.079165

; Move to end of segment 2, extruding 1.195337mm of filament
G1 X6.545000 Y-0.425000 E1.195337

; The next neighboring segment starts where we stopped, so there is no need for an
; empty head move. (6.545000, -0.425000, 0.300000) -> (6.545000, -4.575000, 0.300000) 
; Move to end of segment 3.
G1 X6.545000 Y-4.575000 E1.274502

; The next neighbor again starts where we stopped, so again print segment 4 without a head travel
; (6.545000, -4.575000, 0.300000) -> (0.455000, -4.575000, 0.300000)
G1 X0.455000 Y-4.575000 E1.390674

Determining how much to extrude

How much filament to extrude depends on the filament diameter, nozzle diameter and distance to travel.

filamentArea = 3.14159f * filamentDiameter^2 / 4;
extrusionVolume = nozzle_diameter * layer_height
extrusionFactor = extrusionVolume / filamentArea * extrusion_multiplier

Amount to extrude = extrusionFactor * distance